Teaching Assistants (TAs): ���俫 ���T �L�ۧ� ������
Time: �g�G 14:00~16:50
Place: �g�G ��j�� TR A203
TA Class: �g�G 13:00~13:50 (��j�� TR A203)
Video List: Link
�Фj�a���[�ݥh�~���ҵ{���мv��: https://youtu.be/pLTIKYN2DUg
*�[���зV��A�]���C�g��g�@�~6-10�D�A����G�D�@���F�C�g�u �W�{���@�~3�D�A�ܤ֧����@�D�F�C�g�U�нҵ{���ճ��i�@�p�ɡA�ݤW�ǧ@�~���D��v���C
*��ij�i�H�ĥΥ��ݲ��D�A�M��A��v�����Ƿ|�ѨM���D�N���覡�DzߡA�ĪG����!
Scope:
- Many Classical Algorithms
- Several Machine Learning/Deep Learning Algorithms
- Few Quantum Algorithms (2021�s�W)
- ������(���R�P�]�p����)(25%)
- ������(���R�P�]�p����)(30%)
- �{���]�p�@�~�B���i�B�ҵ{�ѻP�פε{���]�p�v�ɦ��Z(45%)
- 6/15-6/22
Final Examination
(�ɶ�: 6/15 20:00-6/22 12:00)
���5�Ӻt��k���ܤ�2�Ӷi���@�W�Ǧ�Online Judge(���`��14%)�A�䤤1�Ӻt��k�ݭn���g���i�A�Բӻ����t��k�C�ӨB�J����@�L�{�A�ѭ����i�Hdocx��pdf�ɮ榡ú��(���`�� 8%)�C��@���t��k��6/15�ߤW20:00���i�A�{���W�ǻP���iú��I������Ҭ�6/22����12:00�C - My Book's Manuscript -- New Quantum Algorithm Chapter: AlgBook-2021-0617.zip (updated 2021/06/17)(06/17�Ҷq�ɻ~���ءF06/15�s�W Quantum Algorithm���e)(���s���`���e �ɻ~�[������...�A �C�|�ɻ~�ЦC����������έ��X�ýХ��d�M�O�_�w���L�H�C�|�L�C:)
- Term Report (���`�� 8%): Due Day: 06/29
20:00:
�Ьݧ��W�C�Ь�Ѥ������q�l�t��k���s���`�A�w��H�U�D�D���@(��A��B�A�h�g���[��)���g3-5�����������i�A�Y ���ޭz�n�е��õ����X�B�A�H�K�Q�{�w�����i��ŧ :
A. �q�l�{���y��(��ܥH�U�y�����@�A�pQVM�BQCL�BQ#�BQ|SI>�BQ language�BqGCL�BQMASM�BScaffold�BSilq�BLIQUi|>�BQuipper�BfunQ�Ψ�L�y��)
B. �q�l�p��P��줧����(��ܥH�U���Τ��@�A�p�����w���B�Ī��}�o�B���īؼҡB��q�̨ΤơB�Ѯ�w���B����ܾE�B�q�l�����DzߩΨ�L����)
- Term Project Due Day: 06/29 20:00
- My Book's Manuscript: AlgBook-2021-0426.zip (updated 2021/04/26)(��8�������٦b�s�פ��A�Х����n�i��ɻ~)(04/26 �D�n�s�W��8�����y�P�ץ���8���������~)(04/20 �D�n�]�t�Ҧ��ɻ~�ץ��H�έקﬡ�ʿ�ܺt��k�Ψ�ɶ������פ��R)(04/15 �D�n�ץ���k�p����(�����)selection alg.���~�A �ק�heap sort alg.������Huffman coding alg.�PDijkstra alg.�����ϥ�heap-based priority queue�������F04/13�ק�ѦW�A�W�[��0���A�@��0~14���t3�����A ���W�[ ��**�N���|�b�s�褤)(�Ь�Ѱɻ~�[������...�A �C�|�ɻ~�ЦC��������έ��X�ýХ��d�M�O�_�w���L�H�C�|�L�C:)
- R.C.T. Lee et. al., Introduction to the Design and Analysis of Algorithms -- A Strategic Approach (2/e), McGraw Hill, 2005.
- Thomas Cormen, Charles Leiserson, Ronald Rivest and Clifford Stein, Introduction to Algorithms (3/e), MIT Press, 2009.
- �i����, �q�l�q���P�q�l�p��, �֮p, 2020.
- ���ا�(Ķ), �q�l�p����, �֮p, 2020.
- �L�j�Q, TensorFlow + Keras �`�DzߤH�u���z�������, �պӤ��, 2017.
- ���ñd��, Deep Learning -- ��Python�i��`�Dzߪ���¦�z��@, O'REILLY, (�d�Ū�
Ķ, �֮p��T�X��), 2017.
- Algorithm Design: Foundations, Analysis, and Internet
Examples, Michael T. Goodrich, Roberto Tamassia, Wiley, 2002.
(����Ķ��)
- Computer Algorithms, Ellis Horowitz et. al., Silicon Press, 2008.
- ����Java�{���]�p (�ĤT��) SIM-908A , ������ ��, ���L�X����, 2006.
- ����ɦV��Ƶ��c �X �ϥ�Java�y��, ������ ��, �Q�^�ϮѤ��q, 2005.
- Algorithms, S. Dasgupta, C. Papadimitriou and U. Vazirani,
McGraw Hill, 2008.
- Programming Challenges, Steven S. Skiena and Miguel Revilla, Elsevier, 2003.
- The Algorithm Design Manual, Steven S. Skiena, Elsevier.
2 �w��MinGW C++ Compiler (G++): http://prdownloads.sf.net/mingw/MinGW-3.0.0-1.exe?download
3 �w�˳̷sPython 3 Interpreter: https://www.anaconda.com/
4 �w��Jeep7(Java editor for every programmers v7.0) (�U��: Jeep7Setup&SourceCode.exe) (���r�n��|�~�P�����w���n��A���O�Ҧw���A�Цw�ߨϥΡC)
5 �]�w���|�Ѽ�: �`�N�A�o�|�]���A�w�ˤW�C���P�n�骺���P�����Ӥ��P�A�]�|�]���A�w�˪��@�~�t�Ϊ������P�Ӥ��P�C�H�U���w��Windows�@�~�t�Ϊ��]�w:
��� [����x][�t�ΤΦw����][�t��][�i���t�γ]�w][�����ܼ�]�A��X[path]�ܼƨë��U[�s��]�A�æb���ܼƭȥ��ݥ[�J�H�U���e:
;JDK�w�˥� ��\bin;MinGW�w�˥ؿ�\ bin;Python�w�˥ؿ�;Jeep7�w�˥ؿ�
(�Ҧp: ;C:\Program Files\Java\jdk-9.0.4\bin;C:\MinGW\bin;C:\Users\yourname\Anaconda3;C:\Jeep7)
6 �U���d�ҵ{��(Sample.c)(Sample.cpp)(Sample.java)(Sample.py)�x �s��C:\Jeep7�ؿ����A���U�ୱJeep7�ϥܰ���Jeep7�n��A�èϥ� [�}����]�ﶵ���J�d�ҵ{���i��[�sĶ][����]�C
- The
Universidad
de Valladolid (UVa) judge: http://online-judge.uva.es
Example: http://online-judge.uva.es/p/v100/10041.html (Vito's Family) (Vito.java) (Vito1.java) (Vito.cpp)
Exercise: http://online-judge.uva.es/p/v102/10258.html (Contest Scoreboard)
Exercise: http://online-judge.uva.es/p/v5/531.html (Compromise)
- 1. �{�Ѻt��k -- �q���Ш찪���{���y��: (AlgSmallTalk.pptx) (Alg-Intro.pptx) (CPSforIndustry4.0.zip) (ACM-ICPC&EPC.ppt)(CPSProject.zip)(3/2) 1. �t��k�W�٪��Ѩ�
2. ����O�t��k?
3. �t��k���Ҥl
4. �p����ܺt��k?
5. �p���@�t��k? (EuclidGCD.c)(EuclidGCD.cpp)(EucidCGDClass1.java)(EucidCGDClass.java)(EuclidGCD.py)
6. �t��k�����T��
Homework1: (for 3/2; Due day: before next class or TA's class)
(A)�ϥε�����(pseudo code)�g�@�Ӻt��k�A��J�@�Ӿ��n(n>2)�èçP�_n�O�_�����(prime)(Write an algorithm using the pseudo code to input an integer n and output (decide) if n is a prime.)
(B) �ϥε��� ��(pseudo code)�g�@�Ӻt��k�A��J�@�Ӿ��n(n>2)�ÿ�X�p��n���̤j�]��(factor) (Write an algorithm using the pseudo code to input an integer n and output the n's largest factor that is less than n.)
(C) �ϥε��� ��(pseudo code)�g�@�Ӻt��k�A��J�@�Ӿ��n(n>2)�ÿ�X�Ҧ�n���F�����H�~�����]��(factor)�`�M (Write an algorithm using the pseudo code to input an integer n and output the total summation of all n's factors except n.)
(D) �ϥε�����(pseudo code)�g�@�Ӻt��k�A��J���n��m(n>m>2)�A��X�Ҧ���n�p�äj��m��n���]��(factor)�`�M�A�Y�L ���]�ƫh��X0 (Write an algorithm using the pseudo code to input integers n and m, and output all n's factors larger than m and less than n.)
(E) �ϥε�����(pseudo code)�g�@�Ӻt��k�A��J�@�Ӿ��n(n>2)�çP�_n�O�_��������(perfect number)�C�@�ӧ����ƬO�@�ӥ���ơA���Ҧ����u�]��(�Y���F�ۨ��H�~���]��)���M�A��n�������C (Write an algorithm using the pseudo code to input an integer n and output (decide) if n is a perfect number. Note that a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself.)
(F) �ϥε�����(pseudo code)�g �@�Ӻt��k�A��J�@�Ӿ��n(n>0)�çP�_n�O�_���ּּ�(happy number) (Write an algorithm to input an integer n and output (decide) if n is a happy number.)
��: �ּּƦ��H�U���S�ʡG�b���w���i���U�A�ӼƦr�Ҧ��Ʀ�(digits)������M�A�o�쪺�s�ƦA���D�Ҧ��Ʀ쪺����M�A�p�����ƶi ��A�̲��G����1�C�� �p�A�H�Q�i�쬰�ҡG
28 �� 22+82= 68 �� 62+82=100 �� 12+02+02=1�A�]��28�O�ּּ�
- 2. �t��k�����פ��R�d��(�H�ƧǺt��k����)(Alg-Analysis.pptx)(3/9)
.1 �t��k���į�
.2 �t��k���ɶ�������
.3 �jO���i�O��
.4 ���C�t��k�ɶ������q��
.5 ���i�O��(asymptotical notation): Big O, Big Omega, Theta
.6 �h�����ɶ��B���Ʈɶ��ΰ��h�����ɶ��t��k
.7 ��w�Ƨ�(bubble sort)�t��k
.8 ���J�Ƨ�(insertion sort)�t��k
Homework 2: (for 3/9; Due day: before next class or TA's class)
(A) �b��w�Ƨ�(bubble sort)�t��k���A�Y�b�Y�^�X�������S�������ƹ�աA�h�i����Ƥw�g�Ƨǧ����ӥߧY�����t��k����A�o�٬���}��w�Ƨ�(improved bubble sort)�t��k�C���H�����X�y�z�u�� �}��w�ƧǺt��k�v�C(�Ъ`�N:�b���Ǥ��m���A�ҿ� �u��w�Ƨ��t��k�v�������O�u��}��w�ƧǺt�� �k�v)
(B) ���R��}��w�ƧǺt��k�̨ΡB�̮t�P�����ɶ�������
(C) �ϥε�����(pseudo code)�g�@�Ӯɶ�������O(sqrt(n))���t��k�A��J�@�Ӿ��n(n>2)�ÿ�X�Ҧ�n���F�����H�~�����]�� (factor)�`�M�A�A�������R�t��k���ɶ������סC
(D) �ϥε�����(pseudo code)�g�@�Ӯɶ�������O(sqrt(n))���t��k�A��J���n��m(n>m>2)�A��X�Ҧ���n�p�äj�� m��n���]�� (factor)�`�M�A�Y�L���]�ƫh��X0�A���R�t��k���� ���P�Ŷ������סC
(E) �ϥε�����(pseudo code)�g�@�Ӯɶ�������O(sqrt(n))���t��k�A��J�@�Ӿ��(n>2)�çP�_n�O�_�������� (perfect number)�A�A�������R�t��k���̮t�γ̨ήɶ������סC
(F) �ϥε�����(pseudo code)�g�@�Ӻt��k�A�H��J�@�Ө㦳n�Ӥ��������XS�ÿ�XS��幂��(pwoer set)�A�A�������R�t��k���ɶ������סC (Write an algorithm to input a set S of n elements and output the power set of S. You must analyze the time complexity of your algorithm.)
(G) ���R�O�B�Ǧ�ƦC�t��k�P���j�O�B�Ǧ�ƦC�t��k���Ŷ� ������
**(H) �� �ε����X�g�X��n�Ƨ�(heap sort)�t��k�A���R��ɶ��P�Ŷ������� (heap sort���C�J�Ҹսd���A ���O�H�U�C�J�Ҹսd��: �Hbinary heap��@��priority queue��operations�A�]�A insert(p): Inserts a new element with priority p; extractMax(): Extracts an element with maximum priority; remove(i): Removes an element pointed by an iterator i; changePriority(i, p): Changes the priority of an element pointed by i to p; ���㦳O(log n)��time complexity�F��getMax(): Returns an element with maximum priority; �h�㦳O(1) time complexity�C)
(I) �e�Xn log n�Bn log2 n�Bn2��n3�� ��(for n=2, 4, 8, ..., 128)�����C(�s�W)
(J) �Y�@�t��kA���ɶ�������6 x 2n=O(2n)�i�H�bn=10���ɭԯӶO�@�p�ɸѨM���D X�A�ӥt�@���ѨM���DX���t��kB���ɶ�������5 x n3 = O(n3)�A �h�а���n=10���t ��kB�n�ӶO�h�֮ɶ�����?(�s�W)
(H) �Y�@�t��kA���ɶ����� ��6 x 2n=O(2n)�i �H�bn=10���ɭԯӶO�@�p�ɸѨM���DX�A�ӥt�@���ѨM�� �DX���t��kB���ɶ� ������5 x n3 =O(n3)�A�h�а���n�� ��Ȯɺt��kB�n�ӶO�@�p�ɤ~�i�H�� ��?(�s�W)
- 3.
���v(divide-and-conquer)�t��k: (Alg-Divide&Conquer.pptx)(3/16)
�Y�O���D �W��(problem size)���p�A �N�����ѨM���F�Ϥ��A�Y���D�W�Ҹ��j�A�N�N�����(divide)����өΦh�Ӥl���D(���ζ��q)�A�M��N�C�Ӥl���D���j�a (recursively)�� �A(conquer)�ѨM��(���A���q)�C����A�N�C�Ӥl ���D���ѵ��X��(merge)�A�Ϩ䦨������D���ѵ�(�X�ֶ��q)�C.5 �̤j�s��l�ǦC�M(Maximum Contiguous Subsequence Sum, MCSS)�t��k
.1 ���v�t��k²��
.2 ���v�ʳ��ѽL��(tiling a defective chessboard)�t��k
.3 �X�ֱƧ�(merge sort)�t��k (�ݤ��v�t��k)
.4 �ֳt�Ƨ�(quick sort)�t��k (�ݤ��v�t��k)
Homework 3: (���g��3A-3F����@�D�A�[�W�W�g��2A,2B, 2I,2J, 2H����@�D)
A. ���R�X�ֱƧǺt��k���N��Ӥ����̧ǥѤp�Ӥj�ƦC���l�}�CL�PR�X�֬������̧ǥѤp�Ӥj�ƦC���}�CA���ɶ� ������O(n)�A�䤤|L|=|R|=n/2, |A|=n�C
B. ���R�ֳt�ƧǺt��k�̨Ϊ��p�Ŷ�������(best case space complexity)�C
C. ���R�ֳt�ƧǺt��k�̮t���p�Ŷ�������(worst case space complexity)�C
D. �|�X��Ӥ�k���ֳt �Ƨ�(quick sort)�t��k�קK���ͳ��a���p�C
E. ���w�@�ӧǦCS=(-2, 1, -3, 4, -1, 2, 1, -5, 4)�A���merge sort������L�{�e�� �����ϥΤ��v�̤j�D�ųs�� �l�ǦC�M�t��k�D�X�̤j�D�ųs ��l�ǦC�M���L�{�C
F. ���w�@�ӧǦCS=(-2, -1, -3, -4, -1, -2, -1, -5)�A���merge sort������L�{�e �ϻ����ϥΤ��v�� �j�i�ųs��l�ǦC�M�t��k�D�X�̤j�i �ųs ��l�ǦC�M���L�{�C
- 4. ���v�t��k(2): (Alg-Divide&Conquer.pptx��
�b�q)(FFT.zip)
(3/23)
.1 ���v�ֳt�ť߸��ܴ�(fast Fourier transform, FFT)�t��k
.2 ���v�G���D ��(2D rank finding)�t��k
.3 ���v�G�����j�I(2D maxima finding)�t��k
.4 ���v�G ���̪��I��(2D closest pair of points)�t��k
Homework 4: (�C��ǥͳ��n���g2�D: A�D�������D�AB, C, D, E, F��G�� �h����@�D)
A. �|�һ����@�ӧֳt�ť߸��ܴ������ΡC
B. �g�@�Ӥ��v�t��k�ӸѨM�@�ӵ��w�ƭȶ��X ���D��(rank finding)���D�A�öi������פ��R�C
C. �g�@�����v�t��k�ӧ�X�@�s�bX�b�W���I�����̪��I��(closest pair of points on X-axis)�A�öi������� ���R�C
D. ���w8�ӤG�������I: (1, 4), (2, 2), (3, 5), (4, 8), (5, 6), (6, 3), (7, 9), (8, 7)�A�e�ϻ����ϥΤ��v�G�����j�I�t��k�D�X�Ҧ����j�I(maxima)���L�{�C
E. ���w8�ӤG�������I: (1, 4), (2, 2), (3, 5), (4, 8), (5, 6), (6, 3), (7, 9), (8, 7)�A�e�ϻ����ϥΤ��v�G���D���t��k�D�X�C���I����(rank)���L�{�C
F. ���w8�ӤG�������I: (1, 4), (2, 2), (3, 5), (4, 8), (5, 6), (6, 3), (7, 9), (8, 7)�A�e�ϻ����ϥΤ��v�G���̪��I��t��k�D�X�̪��I��Z�����L�{�C
G. �����p��ϥιw���Ƨ�(pre-sorting)����v�̪�G���I�� (closest pair of 2D points)�t��k�C
4.5 �Y�](Convex Hull)�t��k: (ConvexHull.zip) (3/30)
5. �R�M(prune-and-search)�t��k: (Alg-Prune&Search.pptx) (3/30)
�R�M(prune-and-search)�t��k�]�t�h�����N (iteration)�A�b�C�@�������N���A���R��(prune)��J��ƪ��@����(���]��f����, 0<f<1)�A�ӫ�A���j�a(recursively)�H�ۦP���t��k�b�Ѿl����Ƥ��j�M(search)�X�ѵ��C �b�g�L�@�w���ƪ����N��A ��J��ƪ��W�ұN�|�ܱo�۷��p�A�ӯ�b�`�Ʈɶ���������X�ѵ��C
���]�@�ӧR��-�j�M�t��k���ɶ�������T(n)�A�åB�C���� �N�һݪ��ɶ� ��O(nk)(k���j��0���`��)�A�hT(n)=T((1-f)n)+O(nk)�C�ѩ� 1-f<1�A�ڭ̥i�oT(n)=O(nk)�C
.1 �R�M(prune-and-search)�t��k��������
.2 �G���j�M(binary search)�t��k
.3 ���(selection)�P�����(median)�t��k
.4 ����@��� (constrained 1-center)�t��k
Homework 5:
(A) �|�@��8�Ӥ������}�C���һ����G���j�M�t��k���污�ΡA���O�����̨Ϊ��p�ɶ������ק��� �Ф����B���a���p�ɶ������ק��ؼФ����γ��a���p�ɶ������ק䤣��ؼФ����C
(B) �b����R�M�t��k���A�Y�C�Ӥ��Τl���אּ3�Ӥ����A�h����a���p�ɶ������O�_�̵M�� O(n)�A������?
(C) �b����R�M�t��k���A�N�C�Ӥ��Τl���אּ6�Ӥ����᭫�s���R��ɶ������סC
(D) ���@���R�M�t��k��ɶ������� T(n)=T((7/8)n)+cn2�A �ԲӤ��R��ɶ������רåH�jO�O�����ܡC
(E) �H�R�M�t��k�ѨM�H�U����@��߰��D: (0,0),(1,1),(2,2),(3,3),(4,2),(5,1),(6,0),(2,0)�A��ߦby=0�W�C(�i �H��Tø�ϻ����Y�i)
(F) �H�R�M�t��k�ѨM�H�U����@��߰��D: (0,0),(1,1),(2,2),(3,3),(4,2),(5,1),(6,0),(4,0)�A��ߦby=3�W�C(�i �H��Tø�ϻ����Y�i)
-
���D (���褸�e 281
�͡A�褸�e 233 �~��) �O�����
��Q�a�A�O����j�N�k�a��Q���N���H���C��ɴ��A���B���B�P�B���B���B�Q�B���C���åߡCĬ�������X�n�_�X�a����H�ܯ����Բ���
�Q�A�ϯ���
�Q���~�L�k�V��X�L��������F��B�n�_�X�a������C���O��ӱi���H�F��s��~�浦���A�C���U��ѦX�a�ܯ����ܬ��s��˯��A�� ������o�H������A�v���֧]����C
���D�b�m���D�l�P�s���n�g������:�u�ѫJ�i�����Ӻɡv�A�N��O������i�ƾ㬰�s�A�]�N�O�N�@�Ӿ���X�a�ܯ�������Ƥ����\ �h�s�������A�M�ṳ���Y�ḭ���ˡA�@�I�@�I���v�B�I�����`����A�ӹF���@��
�ѤU���ت��C
���椸�Ҥ��Ъ��t��k�A�]�A�G���j�M�t��k�B����P����ƺt��k�έ���@��ߺt��k�A���ĥΧR�M���D�����ѨM���D�C�o�ӵ����N �O�����u�ƾ㬰�s�A�����Ӻɡv�������C�R�M�t��k�]�t�\�h�����N�A
�C�����N�����էR���T�w��Ҫ���J��ơA�ӫ�A���j�a�q�Ѿl��Ƥ��j�M�X�ѵ��A�Y���M�L�k��X�ѵ��h�A�R���T�w��Ҫ���J��ơC �o�˸g�L�X�����N��A��J��ƪ��W�ұN�|�p�쨬�H�����D�b�`�Ʈɶ���
�����ѨM�A�]�ӱo����D���ѵ��C�@��Ө��A��ӧR�M�t��k���ɶ������P�C�ӭ��N���ɶ������ר㦳�ۦP���q�šA�]���R�M�t��O�@ �Ӧ��IJv���t��k�C
- Term Project �����P�о� (3/30)
(�ЦP�ǰȥ��ⴤ�ɶ��[�ݥѧU�п��s��Term
Project�оǼv���A�������������Dz�/�`�Dz����Ҧw�ˡA�ö}�l���g�{���H����Term Project)
�D��: �`�Dzߤ����g�Ʀr����
��J: �����g�Ʀr��ƶ�(dataset)
��X: �����g�Ʀr���ѷǽT�v(accuracy)
����: �`���Z20%
�ت�: ���ǥͽm�ߨϥβ`�Dz�(deep learning)�ҫ��ѨM�����g�Ʀr���Ѱ��D�C�`�Dz�(deep learning)�ҫ��i���`�ׯ��g����(deep neural network, DNN)�B���n���g����(convolutional neural network, CNN)�B���u���O��(long short-term memory, LSTM)���g�����ιh�����j�椸(gated recurrent unit, GRU)���g�����C
��ƶ�����: (��ƶ��U���s��)
��ƶ��ɮ�handwrite_detect.zip�������g�Ʀr��ƶ��A�]�t�F�V�m��ƶ�(training dataset)�P���ո�ƶ�(test dataset)
�V�m��Ʀ@��2450��
���ո�Ʀ@��1700��
�������ػP�W�d:
Source code(.py)
A short report (.pdf) (�t��)
�����g���ѷǽT�v(accuracy)�A�H�I�Ϥ覡�e�{
Source code���v�����
ú��覡: �бN�Ҧ��ɮ����Y�� .zip ��A�A�W�Ǧ� e-class �@�~ú���
(�W���ɦW:Term_Project_�Ǹ�_�m�W.zip)
ú��ɶ�: �����ҩP���U�@�P�G 20:00�e�I��
�Ƶ� : ���Ť��ۧ�ŧ�A�Y�o�{��ŧ�A�h�H0���p��
��v��: https://drive.google.com/drive/folders/1OiRiTyf5xMbHxlUEg2LUbXT9Z9GqgLZu?usp=sharing
�оǼv��:
�t��k�ҵ{_�� ���Dz����Ҧw�ˤ��оǼv���t��k�ҵ{_Machine Learning_01_DNN
�t��k�ҵ{_Machine Learning_02_CNN
- 6. �g���t��k(greedy algorithm):
(Alg-Greedy.pptx) (4/13)
�g���t��k(greedy algorithm)�@�B�B�a�غc�X�@�Ӱ��D������ѵ��C��C�@�B���ǥѳg�����D����(greed strategy)�W�[�@�������ѵ��짹��ѵ����C�ҿ׳g�����D������: �C�@������ܷ��U�̦n�������ѵ��[�J����ѵ����C
.1 �I�]�t��k(knapsack algorithm) (�a�X0/1�I�]���D��i�H�b��������NP-hard���D)
.2 ���ʿ��(activity selection)�t��k
.3 Huffman�s�X(Huffman coding)�t��k
.4 Kruskal�̤p�ͦ���(minimum spanning tree, MST)�t��k
.5 Prim�̤p�ͦ���(minimum spanning tree, MST)�t��k
.6 Dijkstra�t��k
Homework 6:
(A) �@�ӭI�]�e�q�� 10�A�{�b��5�Ӫ��~�A ���q���O��4�B3�B6�B2�B5�A������O��10�B9�B 12�B4�B8�A�D�I�]����ˤJ�s�H(fractional)���~���̤j���Ȭ���?
(B) ���w 5 �Ӭ��ʡA�䬡�ʰ϶����O�� [0,18), [3, 5), [4, 16), [2, 9), [10, 15)�A�дy�z�p��H���ʿ�ܺt��k��X�̦h���ۮe�����`��m(�����g�Xm���ƭ�)�C
(C) �Q��Huffman �s �X�t��k���H�U�r���s�XA(46%)�B B(7%)�BC (28%)�BD (19%)�C(�Ƶ�:�A�������r���X�{�W�v)
(D) �Q��Kruskal�t��k�D�X�H�U����(graph)���̤p�ͦ��� (minimum spanning tree, MST)

(E) �Q��Prim�t��k�D�X�H�W����(graph)���̤p�ͦ��� (minimum spanning tree, MST)
(F). �Q��Dijkstra�t��k�D�H�U��(graph)���I4��U���I���̵u���|(shortest path)�Ψ�Z��(����)�C��: �ݭn�g�X�C�����N�C�Ӹ`�I���� �u���|��s���L�{�C
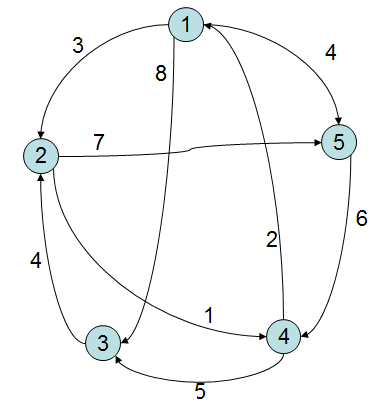
(G). �ӤW�D�A�Q��Dijkstra�t��k�D���I1��U���I���̵u���|(shortest path)�Ψ��Z��(����)�C��: �ݭn�g�X�C�����N�C�Ӹ`�I���� �u���|��s���L�{�C
- ������: (�� ��: 4/20 �U ��2:00-3:50)(�d��: �w�½Ҫ�����:�Ь�Ѳ�0�����7���A�[��9��Dijkstra alg.)(�a�I: ��TA�t�椽�G���Ӯy����J�y�A���ս����f�n)(��v����s���C�A�]���зǵ��ץH�����Ь�Ѭ���: AlgBook-2021-0415.zip ) (�Ь�Ѱɻ~�[������...)
- ���i:
5/12(�P���T)14:00-15:50 �q�l�t��k²���t�� (�a�I: �u���] A207)
6/1(�P���G) 14:00-17:00 �q�l�q���{���]�p�ҵ{ (�a�I: �q�⤤��)(�]���̱�����)
7. �ʺA�W��(dynamic programming)�t��k: (Alg-DP.pptx) (4/27)
�t��k�ҵ{_0427 maximum contiguous subsequence sum, MCSS Dynamic Programming algorithm_6
�ʺA�W��(dynamic programming)�t��k�y�ѱN����D���Ѧ��@�t�C�l���D (subproblems)�A�ȩ̀ǸѨM�l���D�ӸѨM����D�C���קK�@�A�a�ѭ��ƪ��l�� �D�A�@���ѥX�l���D���ѵ�(solution)�A�Y�|�N��s�b����(�ΰ}�C)���C���ݭn�Ψ�Y�@�l���D���ѵ��ɡA�P�䭫�s�p��� �ѵ��A�t��k�|���ӥN���a �q���椤�������X��ѵ��H�`�٭p��ɶ��A�O�@�ӡu�H�Ŷ������ɶ��v���t��k�C�@�ӰʺA�W���t��k�|���q��²�檺�l���D���Ѱ_�A�� �H�@�w���{�ǫ���B�檽�� �D�X����D�ѵ�����C
�̨θѭ�h(Principle of optimality):
���]���F�ѨM�@�Ӱ��D�A�ڭ̥����@�X�@�t�C���M�� D1, D2, �K,
Dn�C�Y�o�@�t�C���M���O�̨θѡA�h�w���en-k��(�γ̫�n-k��)�M���Ҳ��ͪ����A(�l���D)�Ө��A�̫᪺k��(�Ϋek��)�M
��(1<= k<=n)���w�]�O�̨Ϊ��C
*�̪��@�P�l�ǦC(longest common subsequence, LCS or LCSS)�t��k
*�̤p�s�覨�� (Minimum Edit Cost, MEC)�t��k
*0/1�I�]�ʺA�W���t��k(0/1 knapsack dynamic programming algorithm)
*�l���X�[�`(subset sum)�ʺA�W���t��k
*(�Ʋ�)�h�����ΰ��h�����ɶ��t��k
*�̤j�s��l�ǦC�M(maximum contiguous subsequence sum, MCSS)�ʺA�W���t��k
Homework 7:
B. �]�p�@�Ӻt��k�A�i�H���ͤ@�ӵ��w���XS���Ҧ��i��l���X�C
C. �]�p�@�Ӻt��k�A�i�H��J����m���ǦCX���� ��n���ǦCY�A��Xtrue�άOfalse�A���O �N��X�O�Τ��OY���l�ǦC�C
D. ���w�@��0/1�I�]���D�p�U�F�I�]����W=12�A�B4�Ӫ��~�䭫�q�U��6�B4�B5�B3�A����ȦU��20�B30�B40�B10�A�����ǥѰʺA�W���t��k �ѨM��0/1�I�]���D���L�{�C
E. �H�l���X�[�`�ʺA�W���t��k�ѨM�H�U�l���X�[�`���D: ���w��ƶ��XS={1, 2, 4, 7}�ξ��c=10�C
F. �ק�l���X�[�`�ʺA�W���t��k�Ϩ�Ǧ^�[�`�Ȭ�c���l���X�Y���l���X�s�b�F�_�h�Ǧ^�Ŷ��X�C
G. �OS = (-2, 1, -3, 4, -1, 2, 1, -5, 4), �ϥ��ʺA�W���t��k�D�X�̤j�s��D�Ťl �ǦC�M�C
H. �]�p�̤j�s��i�Ťl�ǦC�M�ʺA�W���t��k�C
- 8.
(5/4)��j�M(tree
search)�P�^��(backtracking)�t��k: (TreeSearch.pptx)
(5/4)
Slides and Videos: (Alg4-1203(NoMark).pptx) (��: ��v����36�M37�� ��ĤT�h�k�䪺�T�Ӹ`�I�ѥ��ӥk�̧Ǭ�"2' "4' "5") 5/4�ҵ{�v��==>Youtube video:https://youtu.be/mM93FheJEGQ)
*�\�h���D���M��ѵ��L�{�i�H�ϥξ� (tree)�Ӫ��F�A�o�����D�]���i�H�غc �X�ѵ��Ŷ���(solution space tree)�C�]���n���o�ǰ��D���ѵ��A���ެO�i���(feasible solution)�άO�̨θ�(optimal solution)�A�N���ܦ��@�Ӿ�j�M(tree search)���D�C
*���\�h��k�i�H���X(visit)�P�ݮi(expand)�@���ѵ��Ŷ���A�]�A�`���u���j�M(depth- first search, DFS)�B�s���u���j�M (breadth- first search, BFS)�B�n�s�j�M(hill climbing search, HCS)�H�γ̨��u���j�M(best-first search)���t��k�C
* �s���u���j�M(breadth-first search, BFS)�t��k
* �`���u���j�M(depth-first search, DFS)�t��k
* �n�s�j�M�k(hill climbing search, HCS)�t��k
* �̨��u���j�M�k(best-first search)�t��k
* �^��(backtracking)�t��k
Homework 8:
A. ���w�@���XS={7, 4, 1, 2, 11}�H�Τ@�[�`��10�A�Q�β`���u���j�M�k�ӸѤl���X�[�`���D�A�A�����e�X�ѥX���D���� ���Ŷ���(solution space tree)�C
B. �H�`���u���j�M�t��k��X�H�U�� (graph)���~�̺��y�j�� (Hamiltonian circuit)�A�A�����e�X�ѥX���D ���� ���Ŷ���(solution space tree)�C
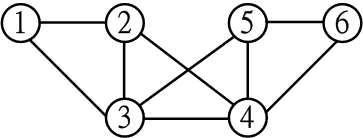
C. �H�s���u���j�M�t��k��X�W�Ϫ��~�̺��y �j���A�A�����e�X�ѥX���D ���ѵ��Ŷ���(solution space tree)�C
D. �H�ų� �檺���ʤ�V���W�U���k�����ǡA�H�s���u���j �M�t ���k�U�ѨM�H�U ���K����(8- puzzle)���D�C
�_ �l���A:
�ؼЪ��A:2
3184765
E. �H�ų� �檺���ʤ�V���W�U���k�����ǡA�H�`���u���j �M�t ���k�ѨMD�D�� ���K����(8- puzzle)���D�C1238
47
65
F. �H�ų�檺���ʤ�V���W�U���k�����ǡA�H�n�s�j�M�t���k�ѨMD�D�����K����(8-puzzle)���D�C��������Ƭ� ������m���ƥءA�Y���ۦP�� ���ΡA�h�H�ų�����ʤ�V�W�U���k�����u�����ǡC
G. �H�ų�檺���ʤ�V���W�U���k�����ǡA�H�̨��u���j �M�t���k�ѨMD�D�����K���� (8-puzzle)���D�C��������Ƭ�������m���ƥءA�Y���ۦP�����ΡA�h�H�ų�����ʤ� �V�W�U���k�����u�����ǡC - 9. (5/11)
����w��(Branch and
Bound)�t��k (Branch&Bound.zip)
(Youtube video Part1: https://youtu.be/KUlDxRV6fsU)(Youtube video Part2: https://youtu.be/R91wC81n6Yk)
(5/11)
*����w��(branch and bound)�O�@���� �X�P�ݮi�� ���Ŷ��𪺯S����k�A�Ω��X���D���̨θѡC�䰵�k�۷����X�@�ؤ�k�Ӥ��ΥX�ѵ��Ŷ�������(branch)�A�M��H�W�� (upper bound)�P�U��(lower bound)�������ӥ[�ֳ̨θѪ��j�M�C
*���M��̤p����(minimum cost)�ѵ����̨Τư��D�Ө��A����w�ɺt��k�|�w��C�@���䪺�ѵ��w���䦨���U��(lower bound)�A�çQ�Χ�X�i��Ѩӱo����D�������W��(upper bound)�C�p�G���@�Ӹѵ��������U�ɶW�L���D�����W�ɡA�h�o�ӸѤ��i��O�̨Ϊ��A�]���t��k�|����(terminate)�P �o�ӸѬ����p����Ӥ��䪺 �j�M�C
*�ӹ��M��̤j�Q�q(maximum benefit)�ѵ����̨Τư��D�Ө��A����w�ɺt��k�|�w��C�@���䪺�ѵ��w����Q�q�W��(upper bound)�A�çQ�Χ�X�i��Ѩӱo����D���Q�q�U��(lower bound)�C�p�G���@�Ӹѵ����Q�q�W�ɧC����D�Q�q�U�ɡA�h�o�ӸѤ��i��O�̨Ϊ��A�]���t��k�|����(terminate)�P �o�ӸѬ����p����Ӥ��䪺 �j�M�C
.1 ����
.2 ����w�ɺt��k(�t�X�n�s�j�M�k)�ѨM�h���ϳ̵u���|���D
.3 ����w�ɺt��k(�t�X�̨��u���j�M �k)�ѨM�Ȧ���P�����D
.4 ����w�ɺt��k(�t�X�̨��u���j�M �k)�ѨM0/1�I�]���D
.5 �@�ӯS��������w�ɺt��k: A*�t��k
Homework 9:
A. �H����w�ɺt��k�ѨM�H�U�h���ϳ̵u���|���D�C

B. ���w�@0/1�I�]���D�A��I�]�i����C=10,�B���T���~�����q���O��10, 3, 5�A�Ө�Q�����O��40, 20, 30�A�D�X�i�H��J�I�]�����~�Q�����t�Ȫ��̤p�ơA�ϥΤ���w�ɺt��k�ӸѦ�0/1�I�]���D�C �]��: �����e�X�j�M��^(���D�ϥέt���ؼШ�ƭȡA�]��feasible solution�O�D�Xupper bound�A�ӥB�ڭ̤��_ �a���խ��Cupper bound)
C. �P�W �D�A���ؼЧאּ�D �X�i�H��J�I �]�����~�Q�����̤j�ơA�ϥΤ���w�ɺt��k�ӸѦ�0/1�I�]�� �D�C �]��: �����e�X�j�M��^(���D�ϥΥ����ؼШ�ƭȡA�]��feasible solution�O�D�Xlower bound�A�ӥB�ڭ̤��_�a���մ���lower bound)
D. �ϥ�A*�t��k�ӸѥH�U���h���ϳ̵u���|���D�C�]��: �����e�X�j�M��^

E. �NA�D��S�PT��աA�b�Y�ϦV���D�C
F. �NB�D�Ҧ��������H2��3���D�C
G. �NC�D�����~���q�אּ20, 5, 6���D�C
H. �ND�D��V0�PV8��աA�b�Y�ϦV�ѥ�V8��V0���̬q���|���D�C - 10.
(5/18)�ϥγg��(greedy)�t��k�H
�ΰʺA�W��(dynamic programming)�t��k�ѨM�̵u���|���D: (Alg-SP.pptx) (5/18)
�ѥ[�v���V��(weighted digraph)�����Y�ӳ��I�θ`�I (vertex or node)v��Ϥ����t�@�`�Iu�A�Yv��u�����s�b�@�����|(path)�A�h���|���Ҹg�L����(edge)���v��(weight)�`�X�٬����|������ (cost)�ζZ��(distance)�A�өҦ����|���㦳�̤p�����ζZ�������|�h�٬��̵u���|(shortest path)�C
�ۦW���̵u���|�t��k�]�A�G
(0) �����ҵ{���n����(�t�g���t��k�ΰʺA�W���t��k���������)(�v�����}:https://youtu.be/YYg8iLf1ej4)
(1) �h���ϳ̵u���|�t��k(�ϥΰʺA�W�����D����)(�v�����}:https://youtu.be/GQ4xKH4MpYI)
(2) Dijkstra�t��k(�ϥγg�����D����)(�����ҫe�w�ѻ��A�]�����]�t�b�����ҵ{�v����)
(3) Bellman-Ford�t��k(�ϥΰʺA�W�����D����)(�v�����}:https://youtu.be/jc-NLpcV6vY)
(4) Floyd-Warshall�t��k(�ϥΰʺA�W�����D����)(�v�����}:https://youtu.be/UdTjmFy7J_E)
Homework 10:
A. �ϥΰʺA�W���t��k�D�H�U�h���Ϫ��̵u���|�C
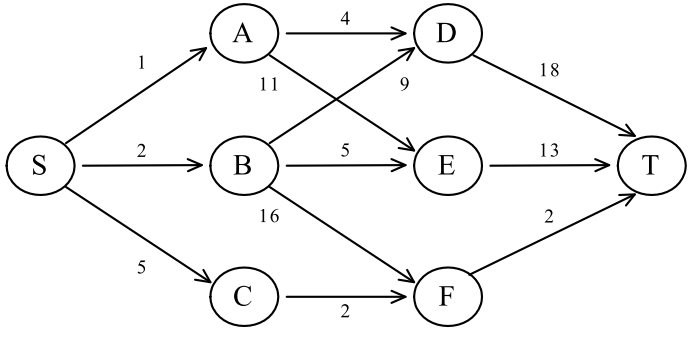
B. �Q��Dijkstra�t��k�D�H�U��(graph)���I4��U���I���̵u���|(shortest path)�Ψ�Z��(����)�C

C. �ӤW�D�A�Q��Dijkstra�t��k�D���I1��U���I���̵u���|(shortest path)�Ψ��Z��(����)�C
D. �e�ϻ����Q�ΧQ��Floyd-Warshall�t��k�D�H�U��(graph)����̵u���|(all-pair shortest path)�Z��(����)(���Ϫ��ҩl�Z���x�}�p�U�A�H�g�L�������`�I��s, a, b, c, d�����Ǽg�X�Z���x�}�����ܹL�{�C)
(d->b���[�v�b�ϧλP���椤�~�Ӭ����@�P���ȡA�P�ǥi�H�N���אּ5��6���ϧλP����@�P����D�����C)
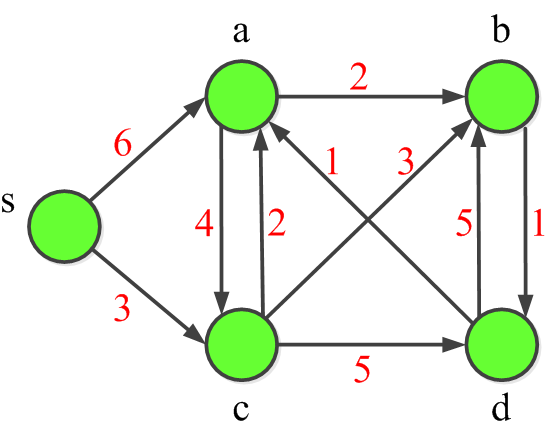
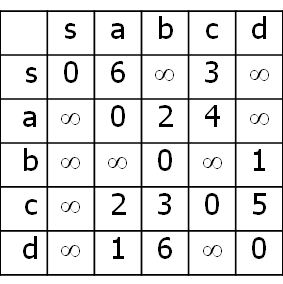
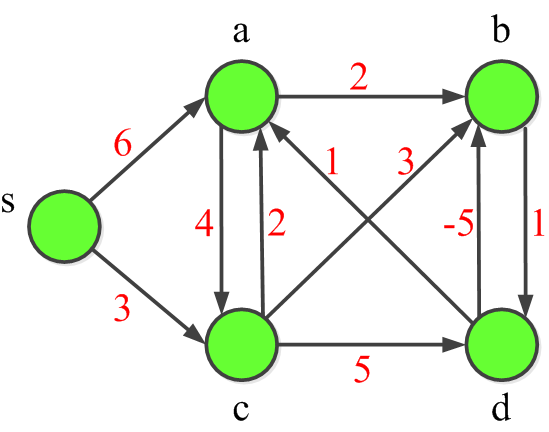
E. �D�X�H�U���w��(graph)��Floyd-Warshall�t��k���ҩl�e�`�I�x�}(�}�C)�A�èD�X�̫᪺�e�`�I�x�}(�} �C)�C

G. �w��H�U�����w�ϡA�C�XBellman-Ford�̵u���|�t�� �k����L�{�A ����Bellman -Ford�̵u���|�t��k�p���ˬd�X�@���w�Ϩ㦳�t�`��(negative-weight cycle)�C
- (��
�ά��� �t��k�����פ��) (Optional)
- Introduction to Software Defined Networking (SDN) Multicast (SDN-Multicast.pptx) (Optional)
- 11. (5/25)(6/1)��
�D�U�ɻP���D����: P�BNP�BNP�x���PNP�������D (5/25)(6/1)
*�@�Ӱ��D ���U�ɬ������ѨM�����D���t��k�ܤ֩һݪ��ɶ������סC(The lower bound of a problem is the least time complexity required for any algorithm which can be used to solve this problem.)
*NP�������D�z��: �Y����@��NP�������D�i�b�h�����ɶ��Q�ѨM�A�h�C�@��NP���D�ҥi�b�h�����ɶ���o�ѨM(�]�N�OP=NP)�C If any one NP-complete problem can be solved in polynomial time, then every problem in NP can also be solved in polynomial time (i.e., P=NP). (ProblemLB.zip)(Recipe, Cook and Carp)(NPC.zip)
*(NPC�z�״���θѵ�)
��6/1(�P���G) 14:00-17:00 �x�j�q�l�q���{���]�p�ҵ{�]���̱������A��^�ѦѮv�u�W�W�ҡC
(5/25���ҵ{���[�ݤU�C���v���A�@ �~��A-F)
�t��k�ҵ{_0525_1(13:00'����L�Z�Ŭ������e�A�� ��13:00'�����[��)
�t��k�ҵ{_0525_2(01:01' ����L�Z�Ŭ������e�A�Х�01:01'�����[��)
�t��k�ҵ{_0525_3(05:41'����L�Z�Ŭ������e�A�Х� 05:41'�����[��)
(6/1 ���ҵ{���[�ݤU�C���v���A�@�~��G-S�A���FS�D���~�Aú�� �@�~�ɶ��������C�Ӱ��D���w�q�A�M��A�g�ҩ�)
Homework 11:
A. �H�U���ԭz�O���٬O���A�ø�����ο�����]:
�Y�ڭ̯��ҩ�����@�� NPC���D�����a���p���D�U��(worst case problem lower bound)�O���ƨ�ƶq�šA�h�ڭ̤w�g�ҩ� NP������P�C
B. �H�U���ԭz�O���٬O���A�ø�����ο�����]:
�Y�ڭ̯��ҩ�����@�� NPC���D�����a���p���D�U��(worst case problem lower bound)�O�h������ƶq�šA�h�ڭ̤w�g�ҩ� NP����P�C
C. �H�U���ԭz�O���٬O���A�ø�����ο�����]:
�Y�ڭ̯ઽ���@�ӽT�w�ʺt��k�A�b�̮t���p�U�H�h�����ɶ������ѨM�@��NPC���D�A�h�ڭ̤w�g�ҩ�NP����P�C
D. �H�U���ԭz�O���٬O���A�ø�����ο�����]:
�H�̤w�g�ҩ�: �S������T�w�t��k(deterministic algorithm)�i�H�b�̮t���p(worst case)�U�A�H�h�����ɶ������ѨMNPC���D�C
E. �H�U���ԭz�O���٬O���A�ø�����ο�����]:
�H�̤w�g�ҩ�: �S������T�w�t��k(deterministic algorithm)�i�H�b�̮t���p(worst case)�U�A�H�h�����ɶ������ѨMNP-hard���D�C
F. �H�U���ԭz�O���٬O���A�ø�����ο�����]:
����NPC���D�i�Hpolynomially reduces to�t�@��NPC���D�C
G. �ҩ���t�����D(dominating set problem)��NP���D�C�ҩ���t�����D(dominating set problem)��NP���D�C
H. �ҩ��I�л\���D(vertex cover problem)��NP���D�C
I. �ҩ����ΰ��D(clique problem)��NP���D�C
J. �ҩ��ۦ���D(chromatic coloring problem)��NP���D�C
K. �ҩ�0/1 �I�]���D(0/1 knapsack problem)��NP���D�C
L. �ҩ�3-�������D(3-SAT problem)��NP���D�C
M. �ҩ��̤j�ΰ��D(Max cut problem)��NP���D�C
N. �ҩ��v�Z�S����D(Steiner tree problem)��NP���D�C
O. �ҩ��������D(partition problem)��NP���D�C
P. �ҩ��������X���D(hitting set problem)��NP���D�C
Q. �ҩ��T���ǰt���D(3-dimensional matching problem)��NP���D�C
R. �ҩ�Convex Hull���D�����D�U�ɬ�Omega(n log n)
S. �e�Xmerge sort�t��k���T�Ӥ���(1,2,3)��decision tree
- 12.
�I���Q�t��k(Hungarian Algorithm)(HungarianAlg.zip)(6/8)
�t��k�ҵ{ _0608(�I���Q�t��k)�v��
Homework 12: ���g�u�����D�A�]���C�Ӿǥͳ��n���o���D�@�~�A�����g����ú��v���P²���C
A. �ϥΦI���Q�t��k(Hungarian algorithm)�ӸѥH�U���̤p�����������D(assignment problem)�]��: �����g�X�t��k����L�{�����C�Ӥ������G�^
B. �����p��ϥΦI���Q�t��k(Hungarian algorithm)�ѨM�̤p�ڤ��v���t��(Minimum Euclidean Weighted Matching)���D�C�ҿ׳̤p�ڤ��v�� �t����D�y�z�p�U: ���wn���I(n������)�A�p��N��n���I�ǰt�Φ�n/2���I��A���C���I��Φ��@���u�q�A�Ӧ�n/2���u�q�㦳�̤p�������`�M�C
Task A
Task B
Task C
Tim
$1
$2
$3
Bob
$2
$3
$2
Alex
$2
$2
$3
